描き手が「はかり棒」を計測の尺として利用するとき、その尺は絶対的な定規として扱われる傾向にあります。しかし、その尺は完全な精度を保証するものではありません。
これははかり棒を使う時の視点が「眼」であるのに、はかり棒自体の支点は「肩」だからです。
この誤差は、大きい対象を近い距離で描いている場合、プロポーションの計測にはかり棒を使っていると大きな影響を及ぼします。
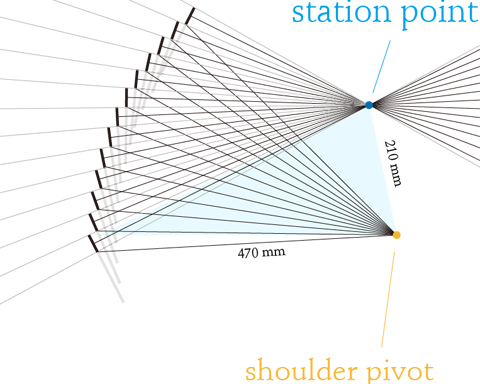
眼と肩の位置が違う分だけ計測の誤差が出る
対象のどこで尺にするかによって、対象の大きさが実際より伸びたり、逆に縮んだりして計測される場合があります。
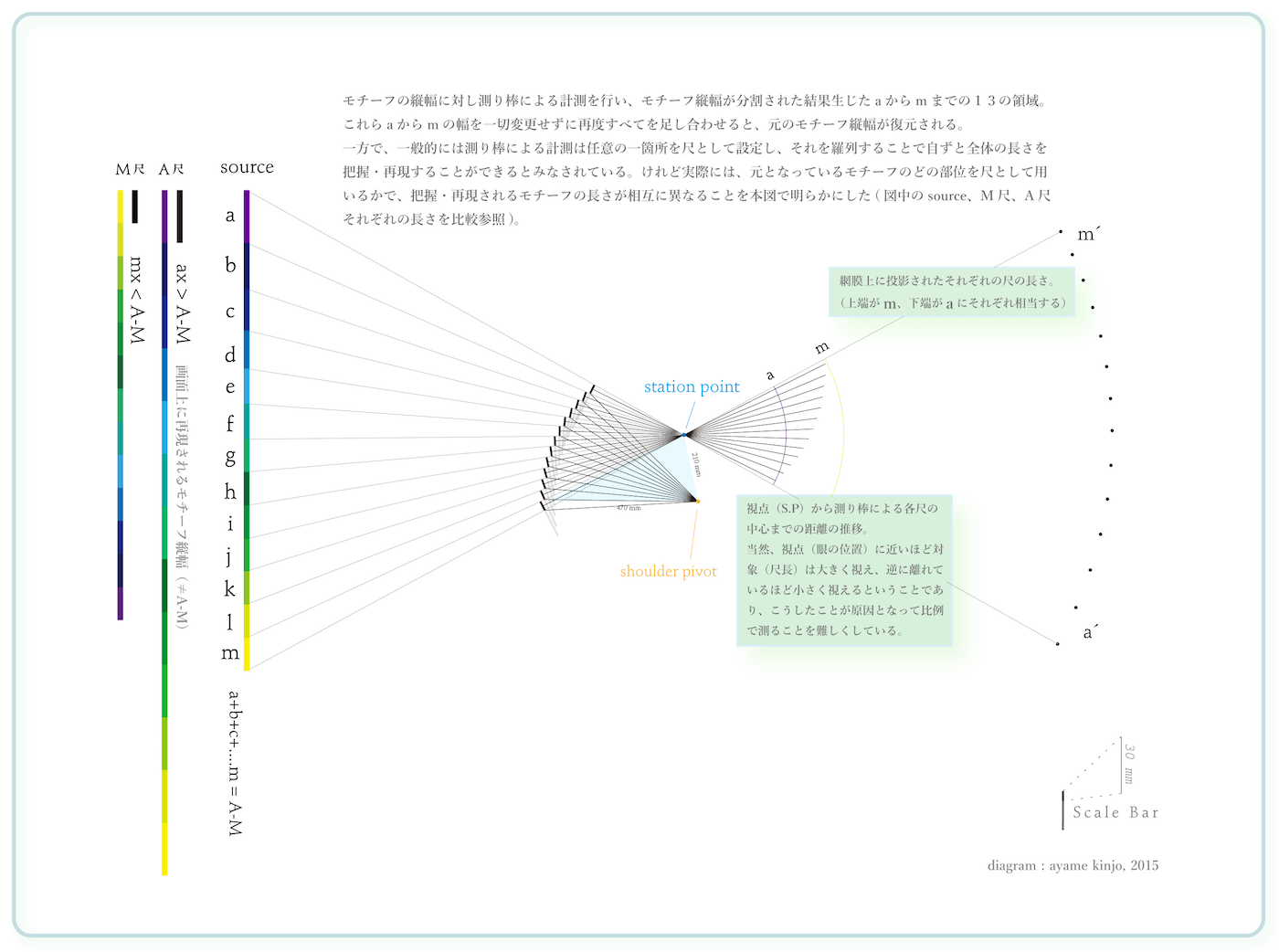
図は、尺であるはかり棒を上下に動かしていく最中に、「眼」と「肩」の動きのズレから尺の長さが変化する様子を説明したものです。「station point(青丸)」は視点である眼を、「shoulder pivot(黄丸)」は支点である肩を表しています。
「station point」から伸びた線と「shoulder pivot」から伸びた線が交差するところにある茶色の太線は、はかり棒の「実際の尺」の長さです。はかり棒の「実際の尺」は視線と直交する必要があるため「station point」から伸びた直線と垂直の関係にあります。
aからmの太線は、眼と肩を上下に動かすことで変化する、はかり棒の「見かけ上の尺」の長さを表しています。「実際の尺」の長さは同じですが、「見かけ上の尺」であるaからmの長さはそれぞれ異なっています。図の場合はaが最も長く見え、mが最も短く見えます。
この図からは以下のことが読み取れます。 「a+b+c+d+e+f+g+h+i+j+k+l+m=AM」とします。aからmまでは13個ですから、aを尺として対象を計測した場合は「a×13=a13」。mを尺として計測した場合は「m×13=m13」です。 その長さの関係は、「a13>AM>m13」となります。
今回のケースであれば、aを尺とした場合は、対象の低い位置ほど間延びして観測され、mを尺とした場合は対象の高い位置ほど圧縮されて観測されることになります。
また、この計測のズレは上下だけでなく、横方向にも言えることです。目と肩の位置は横方向にも差異があるからです。
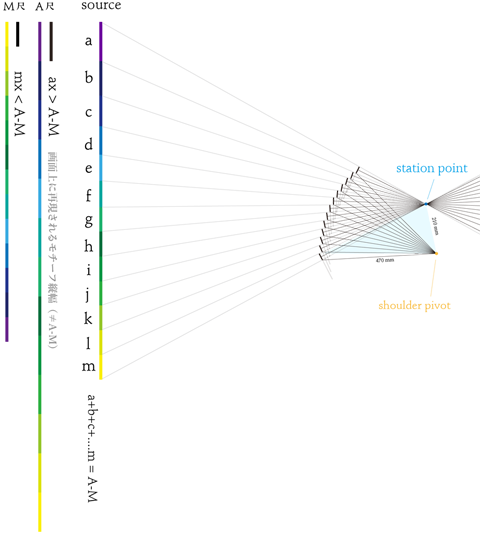
近くて大きな対象を描く時は誤差が目立つ
「見かけ上の尺」が異なることは明らかになりましたが、そのズレがどれほど大きいのかは、描き手と対象の距離に加え、対象の大きさによっても違ってきます。そのため、場合によっては大きな影響を及ぼさない可能性もあります。
これは先ほどの図を応用し、描き手である「station point」と「shoulder pivot」を対象であるAMに近づけたり、離したりすることでわかります。
例えば、描き手と対象の距離が遠いほど、この誤差は目立ちません。逆に、すぐ目の前にある大きな対象を計測する場合は、明らかな形の狂いとわかるほどの誤差として目立つ可能性があります。
それでもはかり棒を使った方がよい
上述の結果を見て、「じゃあ、はかり棒は使わないでおこう」と思うのはもったいないことです。
初学者が目測だけで対象の形を合わせるのは難しいです。目測の精度をあげるために、確認作業としてはかり棒で計測することには大きな利点があるからです。
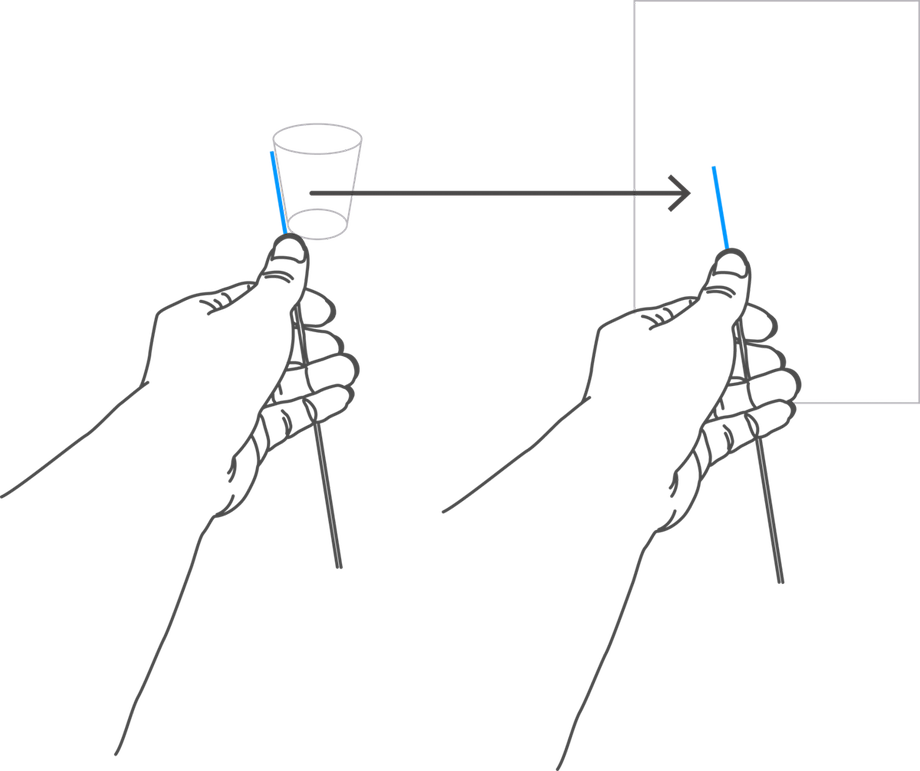
ただ、大きな対象を描いたり、近距離で描いたりする場合、はかり棒でプロポーションを測るのはやめておきましょう。誤差が大きく出ます。そのような場合は、はかり棒を使って対象の形の傾き具合を計測するようにしてください。傾きを測る場合には上述のような問題は起きないからです。
また、もしあなたが誤差の大きさに関係なく、はかり棒でプロポーションを計測するのは不安だと思うのなら、傾きや角度を計測する時にのみはかり棒を利用してください。